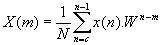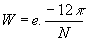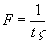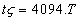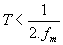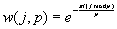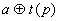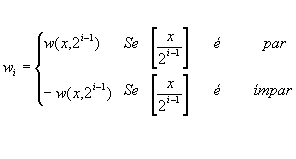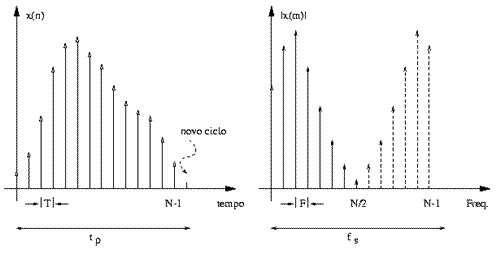
Palavras-Chaves: Transformada de Fourier, bi-dimensional FFT, processa-mento de imagem.

Resumo

A transformada de Fourier é extensivamente usada em teoria de informação, processo notável e processamento de imagem. A derivação de teoria da transformada de Fourier não é considerada aqui, mas exemplos de sua utilidade no melhoramento de imagem são discutidos.

A teoria da transformada de Fourier assume que o sinal é contínuo com uma extensão infinita, para o qual a transformada é desejada. Por outro lado, imagens são freqüentemente descontínuas ao longo de uma linha ou coluna da imagem. Para analisar dados de pixel de uma imagem contínua a versão discreta de transformada de Fourier foi desenvolvida e foi chamada de transformada rápida de Fourier (FFT). Esta implementação é a base para a maioria de algorítmos de processamento de imagens usando transformada de Fourier.

Qualquer imagem pode ser representada por uma transformada de Fourier bi-dimensional, a qual pode ser considerada como uma imagem com uma parte real e uma parte complexa. A bi-dimensional FFT é um mapeamento de valores de pixel de imagem no espaço de freqüência da imagem espacial. Executando a bi-dimensional FFT em uma imagem, cria-se um mapa bi-dimensional de todas as freqüências de espaço dentro de uma imagem.

Todo pixel de imagem de produção, como resultado da FFT, tem um número real e um número imaginário associado a ele. Os pixels reais formam uma imagem que pode ser analisada como a magnitude do presente de freqüências de espaço em uma imagem, e os pixels imaginários formam a imagem que representa a fase das freqüências de espaço. Como mostrado, a freqüência de espaço mais alta que pode estar presente em uma imagem é equivalente a todo outro pixel que tem valores pretos-e-brancos. Então, se eixos x e y são usados para representar freqüências de espaço em um diagrama, a largura do diagrama vai, no máximo, até a largura total da imagem dividida por 2.

A transformada de Fourier é amplamente utilizada no universo de processamento de imagens. Uma aplicação para sua utilização é analisar imagens e retirar ruídos que se apresentam em uma forma padronizada dentro da imagem. Através da Transformada de Fourier, construímos um diagrama que nos permite analisar padrões encontrados na imagem. Com a transformada inversa, podemos isolar e visualizar somente estes padrões da imagem.

A transformada de Fourier é também de extrema importância no processamento de imagens, processamento de sinais, processamento de sons e inúmeras áreas relacionadas. Devido à gama de utilizações de tal ferramenta e à sua importância em processamento de imagens, uma implementação eficiente pode ajudar em muito qualquer um dos estudos acima.

Embora os algoritmos que implementam a transformada de Fourier sejam relativamente compactos e simples, possuem um número gigantesco de operações complexas, o que torna extremamente lenta a execução em grandes resoluções. Sendo assim, este artigo propõe estudar a implementação de uma técnica de transformada de Fourier que trabalha separadamente com cada dimensão.

A essência do cálculo da Transformada Rápida de Fourier (FFT) é uma série de operações matemáticas conhecida como Transformada Discreta de Fourier (DFT), que é um conjunto m de variáveis no domínio da freqüência a partir de um conjunto n de amostras no domínio do tempo. A figura abaixo ilustra um sinal x(n) com N amostras em intervalos de T segundos.

Para n variando de 0 a N-1, a duração do sinal é:

A DFT de x(n) é definida pela soma finita:

onde:

A função X(m) gera m variáveis no domínio da freqüência com incremento

Os algoritmos de FFT funcionam melhor quando o número de pontos da amostra é uma potência inteira de 2, ou seja: N=2^k, onde k é um inteiro positivo. Um programa que utiliza FFT com a finalidade de análise espectral, apresenta certas particularidades na relação entre a DFT e a transformada contínua de Fourier. Em primeiro lugar, deve-se considerar que o tratamento matemático considera o sinal como se ele fosse periódico, embora o sinal possa ou não ser periódico.

Um algoritmo para o cálculo da FFT deve levar em consideração alguns fatores básicos. Se tomarmos N=4096 amostras em um período, tendo-se o incremento entre cada amostra, então o período

Sendo a Î C^Zn, onde n = 2^k , para k inteiro positivo. Sendo P = {2ⁱ : i = 0,1,...,log₂(n) –1} e pÎ P, define-se o modelo parametrizado t(p), por:

onde :

.

O seguinte algoritmo desenvolve a Cooley- Turkey radix-2 FFT.

a : = a o r _n

for i : = 1 to log₂n loop

a : = a Å t(2^i-1)

end loop

Adverte-se que a definição do modelo t gera dois valores para cada 0 <= j <= n-1. Desta forma, somente 2n multiplicações complexas e n somas complexas são requeridas para o desenvolvimento de a Å t(2^i-1). Como a convolução a Å t(2^i-1) está contida num loop de log₂n interações, são O(log n) somas e multiplicações complexas na formulação da FFT.

Esmiuçando um pouco mais o algoritmo descrito, isto é, convertendo todo o formalismo gráfico para simples algoritmo, temos o programa seguinte em C. Antes de iniciarmos, é importante definir que n é o numero máximo de pontos a calcular(deve ser uma potência de 2), que Vetor[i] me dá o valor do nível de cinza correspondente ao ponto e que i é a coordenada x deste ponto.

A primeira linha do algoritmo corresponde a:

for (i=0; i<=(n-1);i++) {

j=0;

m=Vetor[i];

for (l=0; l<=(log₂(n)-1);l++) {

h=m/2;

j=2j+m-2h

m=h;

}

Vetor[i]=j

}

O restante do programa corresponde a:

for (l=0; l<=n-1; l++) {

b=0;

for(i=0;i<=log₂n;i++) {

for (j=0;j<=n-1;j++) {

t=t(2ⁱ)_j(l)

b=b+Vetor[j]*t;

}

}

Vetor[l]=b;

}

Observe que temos a linha t=t(2ⁱ)_j(l), função que já foi definida anteriormente. Porém, para calcularmos t(2ⁱ)_j(l), utilizamos w(j,p), que deve ser subdividido em parte real e parte imaginária, e, portanto, a variável t, b e Vetor[l] do algoritmo devem possuir duas dimensões (uma para a parte real, outra para a parte imaginária).

O cálculo de t(2ⁱ)_j(l) é simplesmente cinco condições de verificação para saber qual parte da função será calculada, sendo que isto pode ser facilmente implementado utilizando as funções switch/case da linguagem C.

Como já vimos, podemos calcular uma DFT bidimensional através de duas DFT unidimensionais. Analogamente, se quisermos a DFT bidimensional de uma determinada imagem utilizando o mesmo procedimento de DFT unidimensionais, devemos aplicar à imagem a formulação algébrica da FFT unidimensional em simples sucessão.

Contudo, para se executar as operações

A permutação p é estendida à função r:X® X de maneira similar, restringindo suas ações para as linhas de X, definimos:

r_m:X® X

by r_m(i,j)=(p_m(i),j).

Com as definições de r e t completas, podemos especificar a FFT bidimensional em termos da notação de álgebra de imagem.

Se X, r_m e t são especificados acima e aÎ C^x, então o seguinte algoritmo calcula a FFT bidimensional de a.

a:=a o r_m

for i:=1 to log₂m loop

a:=aÅ t(2^i-1)

end loop

a:=a’ o r_n

for i:=1 to log₂n loop

a:=aÅ t(2^i-1)

end loop

â:=a’.

A formulação da FFT assume que a operação do modelo da imagem Å é somente aplicada sobre o suporte do modelo.

Se não for este o caso, a "rápida" formulação usando modelos resultará em uma performance muito pobre.

A formulação algébrica da imagem para a transformada rápida usa transformadas espaciais melhor do que modelos.

A formulação alternada é mais apropriada se a implementação de Å não restringe sua própria operação para o suporte de modelo.

Para a formulação alternada, as variáveis da bi-dimensional FFT permanecem como definido acima.

As imagens w_i Î C^x usadas na formulação alternada são definidas como:

A formulação alternada para a transformada rápida de Fourier usando transformadas espaciais é dada por:

a : = a o r_m

for i : =1 to log₂m loop

a : = a o g_i + w_{i .} (a o f_i)

end loop

a : = a´ o r_n

for i : = 1 to log₂n loop

a : = a o g_i + w_{i .} (a o f_i)

end loop

â : = a´.

Com relação ao algoritmo acima, pode-se concluir que "a" corresponde a uma linha, "log₂m" é o número de colunas que esta linha possui, "a’ " corresponde a esta mesma linha "a" só que em colunas (transposta de "a") e "log₂n" é o de linhas que esta coluna possui.

Note que o uso da transposta a’ antes e depois do segundo loop no algoritmo acima é usado para notação simplificada, não para eficiência computacional. O uso das transpostas pode ser eliminado pelo uso de funções análogas fi, gi e wi no segundo loop que são funções de coluna coordenada de X.

A discussão presente aqui concentra-se em uma otimização geral algébrica da transformada de Fourier. Importantes regras surgem quando otimizando a formulação para específicas implementações. O cálculo da função permutação r n, adiciona o custo computacional da FFT. Cada iÎ {0, 1, ..., n-1}, r n(i) requer O(log2n) operações inteiras. A quantia de aritmética inteira envolvida no processamento de r n é da mesma ordem de magnitude da importância de ponto aritmético real para a FFT. Em conseqüência, associado acima com o bit reverso não é trivial no processamento da FFT, freqüentemente em torno de 10% a 30% do total de tempo de processamento.

Após a verificação de cada um dos métodos apresentados, sua complexidade de implementação e eficiência para o cálculo, fica claro que o método a se implementar deve ser a transformada rápida de Fourier (Fast Fourier Transform).

A complexidade destes algoritmos é relativamente grande, porém com a unidimensional FFT podemos ter a base e compreender o princípio da formulação dos algoritmos da bidimensional FFT, já que esta é uma aplicação da unidimensional FFT nos eixos X e Y. A FFT^- é uma conseqüência da FFT.

Aperfeiçoamentos e otimizações dos algoritmos ainda podem ser estudados, porém já é possível prever uma implementação satisfatória destas funções com os métodos e algoritmos propostos.

BLASS, William E.; HALSEY, GEORGE W. Deconvolution of absorption spectra, New York : Academic Press, 1981. 158 p.

BRACEWELL, Ron N. The Fourier transform and its applications. New York : McGraw-Hill 1965. 381 p.

BRAULT, J. W.; WHITE, O. R. The analysis and restoration of astronomical data via the fast Fourier transform. Astron. & Astrophys, 1971, 13, p. 169-189.

BRIGHAM, E. Oren. The fast fourier transform and its applications. Englewood Cliffs : Prentice-Hall, 1988. 448 p.

COOLEY, J. W.; TUKEY, J. W. An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation, 1965, v. 19, n. 90, p. 297-301.

GABEL, Robert A.; RICHARD A. Signals and linear systems. New York : J. Wiley, 1973. 415 p.

GASKILL, Jack D. Linear systems, Fourier transforms, and optics. New York: John Wiley, 1978. 554 p.

Estudante do 4º ano do curso de Engenharia de Computação da PUC