Simulação - Método de Monte Carlo
Autor: Pedro Luis Kantek Garcia Navarro- GPT
Na questão de entender os muitos sistemas que compõem o mundo moderno, nós usamos cada vez mais a simulação em computador. Seja um sistema natural ou artificial, freqüentemente um ou mais de seus componentes tem um tal comportamento complexo que a única maneira de abordá-lo é assumir que ele é randômico. A técnica óbvia é trocar estes componentes complexos por outros mais simples, seguindo as leis da estatística. Por exemplo, se queremos simular um jogo de vôlei entre dois times equilibrados, podemos obter um modelo simples do jogo jogando continuamente uma moeda: se um time está no serviço e a moeda não lhe favorece, o serviço passa para o time contrário. Em caso contrário, o marcador deste time avança um ponto.
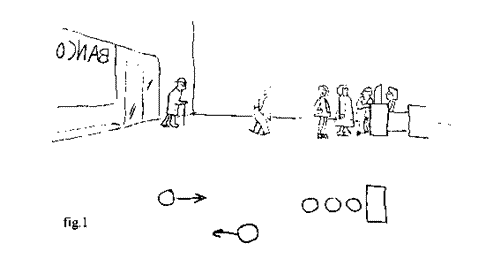
A técnica da moeda nos relembra outro procedimento simples chamado técnica de Monte Carlo. Aqui usaremos um sistema bancário simples para ilustrar as principais características da técnica de Monte Carlo. Considere um banco com um único caixa. Os clientes entram, aparentemente de maneira randômica e formam uma fila na frente do caixa (fig. 1). Abaixo da figura vemos uma versão esquemática da cena como uma indicação de como vários sistemas do mundo real podem ser abstratos.
Em sistemas de simulação bem planejados, uma tremenda quantidade de detalhes inerentes ao sistema original são ignorados sem perda ou penalidade. O comportamento do modelo abstrato quando implementado em computador é indistinguível das coisas reais até onde os parâmetros sob investigação estão envolvidos.
É claro que toda simulação, seja científica ou industrialmente inspirada, deve ter um objetivo e ele determina quais aspectos do sistema sendo modelados são relevantes. No caso da nossa simulação simples no banco, estamos interessados em decidir quando vale a pena adicionar outro caixa.
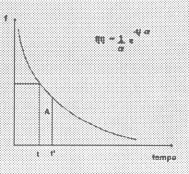
Considerações teóricas sugerem e estudos empíricos implicam que, no mundo real, esta fila de banco, quando no estado estável, tende a receber clientes segundo um padrão de chegada particular. Dado um tempo médio de alfa segundos entre as chegadas, a distribuição destes tempos segue uma distribuição exponencial negativa. (fig.2)
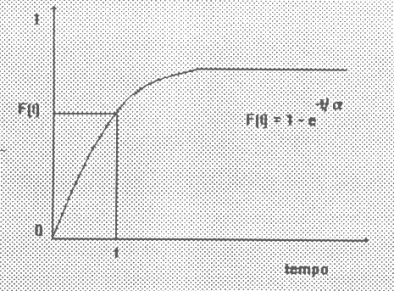
Assim como com qualquer função de densidade, devemos ter cuidado com a interpretação. Para cada possível tempo t entre chegadas consecutivas (tempo interchegadas) a função f dá o que poderia ser chamado densidade interchegadas, mas não a freqüência interchegada como tal. Uma pessoa pode obter alguns intervalos de tempos interchegadas, digamos de t a t', e calcular a área sob a curva. Isto nos dá o número relativo de vezes que alguém pode esperar um tempo interchegada no intervalo t a t'. Então, se queremos predizer para 100 usuários consecutivos quão freqüentemente seu tempo de chegada está num dado intervalo, precisamos simplesmente calcular a área sombreada, e então multiplicar a área por 99, onde 99 é o número de interchegadas. Mas estas considerações não são usadas em computador. Para isto nós precisamos a função de distribuição cumulativa F que é justamente a integral de f. (fig. 3)
Aqui, um dado tempo interchegada t produz uma freqüência acumulada F (t) batizada como a proporção de chegadas tendo tempo t ou menor. Podemos fazer algumas observações interessantes sobre a função F. Se selecionamos números randômicos entre 0 e 1 e então calculamos F-1(x), a quantidade resultado reproduz a função de densidade original f!. Em termos práticos isto significa que se alguém seleciona, digamos, 1000 números randômicos entre 0 e 1 e converte cada um deles pela função inversa F-1, então o histograma das quantidades resultantes tenderá a ter a mesma forma da curva de densidade f mostrada na figura 4.
Esta observação nos habilita a gerar chegadas randômicas no nosso banco simulado, seguindo as etapas 2 a 6 uma vez após a outra.
1. Gere o primeiro cliente
2. Selecione um randômico x entre 0 e 1
3. Compute F-1 (x)
4. Aguarde F-1 (x) segundos
5. Gere o próximo cliente
6. Vá para 2
Números randômicos podem ser gerados por qualquer uma das técnicas conhecidas. Para a função F discutida aqui é fácil mostrar que: F-1 (x) = alfa ln (1-x)
Uma das vantagens da simulação em computadores é que eventos que podem tomar dias ou mesmo meses no tempo real, podem ser extraídos de um computador em segundos, minutos ou, no pior caso, algumas horas de tempo real. Isto é possível porque o fluxo de tempo também é simulado, em muitos casos através de um relógio simulado, uma variável real (digamos C) que mantém uma trilha do tempo. Então no início da nossa simulação na etapa 1, temos C=0. Se o primeiro tempo interchegada na etapa 3 é 137 segundos, então na etapa 4, somaremos 137 a C, atualizando o relógio simulado. A etapa 5, que gera o novo cliente significa simplesmente que devemos adicionar a marca que representa o cliente em alguma estrutura de dados representando a fila na frente do caixa. A simulação deste exemplo não exige que representemos a fila através de algo mais elaborado como um arranjo ou uma estrutura de lista. É suficiente saber em Q quantos clientes estão ocupando a fila. Então quando o computador chega à etapa 5, ele simplesmente adiciona 1 em Q.
Os clientes são retirados da fila, tão logo tenham recebido um serviço completo do caixa. Embora os tempos de serviço encontrados em bancos reais não tenham uma distribuição simples, nós assumimos que eles seguem uma certa distribuição exponencial G, neste caso com uma constante de tempo beta - o tempo médio que o caixa gasta com cada cliente.
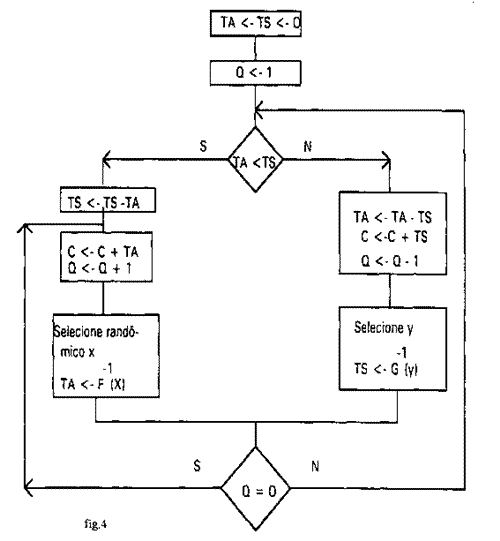
Nós agora estamos em posição de escrever a mesma classe de programas para tempos de serviço como indicado anteriormente nos tempos interchegada. Agora, entretanto, dois tipos de operação devem ser adequadamente intercalados e então cada etapa segue o delineado no fluxo da figura 5. A característica essencial da abordagem é computar o tempo do próximo evento (chegada de cliente ou completamente de serviço) em duas variáveis de tempo TA e TS.
Notemos que TA e TS atuam como dois pequenos relógios. Se TA é menor do que TS, então a chegada ocorre antes e devemos incrementar o relógio da quantidade TA e decrementar o relógio TS da mesma quantidade, já que o tempo (variável C) está correndo, e as duas coisas (chegada e fim de serviço) estão ocorrendo ao mesmo tempo. Após adicionar a nova chegada na fila, geramos o próximo tempo interchegada e anulamos TA. No outro lado do diagrama, os papéis de TS e TA são naturalmente invertidos.
Esta abordagem é denominada técnica do evento crítico. Uma pequena modificação seria simular o tempo da próxima troca no sistema e então fazer o que a troca determina - alterando o tamanho da fila. Outra abordagem para gerenciar o tempo em simulações de computador é chamado método da fatia de tempo. Ela envolve a escolha de incrementos fundamentais pequenos de tempo, que continuamente atualizam o relógio, e para cada atualização percorrem o programa computando o seu novo estado, baseado sempre no estado atual.
O coração do método de Monte Carlo é a geração de novos eventos através da técnica da função inversa. Virtualmente qualquer distribuição, seja teórica na forma de uma função computável ou empírica na forma de um histograma cumulativo, pode ser usada. Com uma estrutura um pouco mais complicada do que a anteriormente vista, qualquer número de caixas pode ser simulado. De fato podemos simular uma multiplicidade de filas, ou uma grande fila única alimentando uma multiplicidade de caixas. Os mais modernos bancos têm adotado esta técnica que sempre gera tempos de atendimento menores. Este sistema também pode ser simulado como uma extensão das técnicas vistas acima.
Existe uma linguagem de propósito especial, denominada GPSS, que é feita para simular sistemas com múltiplas filas, e vários outros tipos de estruturas. É freqüentemente muito mais fácil escrever programas de simulação nestas linguagens, ainda que o tempo de execução costume ser maior do que quando se usam programas especialmente escritos em FORTRAN ou PASCAL.
Na questão de entender os muitos sistemas que compõem o mundo moderno, nós usamos cada vez mais a simulação em computador. Seja um sistema natural ou artificial, freqüentemente um ou mais de seus componentes tem um tal comportamento complexo que a única maneira de abordá-lo é assumir que ele é randômico. A técnica óbvia é trocar estes componentes complexos por outros mais simples, seguindo as leis da estatística. Por exemplo, se queremos simular um jogo de vôlei entre dois times equilibrados, podemos obter um modelo simples do jogo jogando continuamente uma moeda: se um time está no serviço e a moeda não lhe favorece, o serviço passa para o time contrário. Em caso contrário, o marcador deste time avança um ponto.
A técnica da moeda nos relembra outro procedimento simples chamado técnica de Monte Carlo. Aqui usaremos um sistema bancário simples para ilustrar as principais características da técnica de Monte Carlo. Considere um banco com um único caixa. Os clientes entram, aparentemente de maneira randômica e formam uma fila na frente do caixa (fig. 1). Abaixo da figura vemos uma versão esquemática da cena como uma indicação de como vários sistemas do mundo real podem ser abstratos.
Em sistemas de simulação bem planejados, uma tremenda quantidade de detalhes inerentes ao sistema original são ignorados sem perda ou penalidade. O comportamento do modelo abstrato quando implementado em computador é indistinguível das coisas reais até onde os parâmetros sob investigação estão envolvidos.
É claro que toda simulação, seja científica ou industrialmente inspirada, deve ter um objetivo e ele determina quais aspectos do sistema sendo modelados são relevantes. No caso da nossa simulação simples no banco, estamos interessados em decidir quando vale a pena adicionar outro caixa.
Considerações teóricas sugerem e estudos empíricos implicam que, no mundo real, esta fila de banco, quando no estado estável, tende a receber clientes segundo um padrão de chegada particular. Dado um tempo médio de alfa segundos entre as chegadas, a distribuição destes tempos segue uma distribuição exponencial negativa. (fig.2)
Assim como com qualquer função de densidade, devemos ter cuidado com a interpretação. Para cada possível tempo t entre chegadas consecutivas (tempo interchegadas) a função f dá o que poderia ser chamado densidade interchegadas, mas não a freqüência interchegada como tal. Uma pessoa pode obter alguns intervalos de tempos interchegadas, digamos de t a t', e calcular a área sob a curva. Isto nos dá o número relativo de vezes que alguém pode esperar um tempo interchegada no intervalo t a t'. Então, se queremos predizer para 100 usuários consecutivos quão freqüentemente seu tempo de chegada está num dado intervalo, precisamos simplesmente calcular a área sombreada, e então multiplicar a área por 99, onde 99 é o número de interchegadas. Mas estas considerações não são usadas em computador. Para isto nós precisamos a função de distribuição cumulativa F que é justamente a integral de f. (fig. 3)
Aqui, um dado tempo interchegada t produz uma freqüência acumulada F (t) batizada como a proporção de chegadas tendo tempo t ou menor. Podemos fazer algumas observações interessantes sobre a função F. Se selecionamos números randômicos entre 0 e 1 e então calculamos F-1(x), a quantidade resultado reproduz a função de densidade original f!. Em termos práticos isto significa que se alguém seleciona, digamos, 1000 números randômicos entre 0 e 1 e converte cada um deles pela função inversa F-1, então o histograma das quantidades resultantes tenderá a ter a mesma forma da curva de densidade f mostrada na figura 4.
Esta observação nos habilita a gerar chegadas randômicas no nosso banco simulado, seguindo as etapas 2 a 6 uma vez após a outra.
1. Gere o primeiro cliente
2. Selecione um randômico x entre 0 e 1
3. Compute F-1 (x)
4. Aguarde F-1 (x) segundos
5. Gere o próximo cliente
6. Vá para 2
Números randômicos podem ser gerados por qualquer uma das técnicas conhecidas. Para a função F discutida aqui é fácil mostrar que: F-1 (x) = alfa ln (1-x)
Uma das vantagens da simulação em computadores é que eventos que podem tomar dias ou mesmo meses no tempo real, podem ser extraídos de um computador em segundos, minutos ou, no pior caso, algumas horas de tempo real. Isto é possível porque o fluxo de tempo também é simulado, em muitos casos através de um relógio simulado, uma variável real (digamos C) que mantém uma trilha do tempo. Então no início da nossa simulação na etapa 1, temos C=0. Se o primeiro tempo interchegada na etapa 3 é 137 segundos, então na etapa 4, somaremos 137 a C, atualizando o relógio simulado. A etapa 5, que gera o novo cliente significa simplesmente que devemos adicionar a marca que representa o cliente em alguma estrutura de dados representando a fila na frente do caixa. A simulação deste exemplo não exige que representemos a fila através de algo mais elaborado como um arranjo ou uma estrutura de lista. É suficiente saber em Q quantos clientes estão ocupando a fila. Então quando o computador chega à etapa 5, ele simplesmente adiciona 1 em Q.
Os clientes são retirados da fila, tão logo tenham recebido um serviço completo do caixa. Embora os tempos de serviço encontrados em bancos reais não tenham uma distribuição simples, nós assumimos que eles seguem uma certa distribuição exponencial G, neste caso com uma constante de tempo beta - o tempo médio que o caixa gasta com cada cliente.
Nós agora estamos em posição de escrever a mesma classe de programas para tempos de serviço como indicado anteriormente nos tempos interchegada. Agora, entretanto, dois tipos de operação devem ser adequadamente intercalados e então cada etapa segue o delineado no fluxo da figura 5. A característica essencial da abordagem é computar o tempo do próximo evento (chegada de cliente ou completamente de serviço) em duas variáveis de tempo TA e TS.
Notemos que TA e TS atuam como dois pequenos relógios. Se TA é menor do que TS, então a chegada ocorre antes e devemos incrementar o relógio da quantidade TA e decrementar o relógio TS da mesma quantidade, já que o tempo (variável C) está correndo, e as duas coisas (chegada e fim de serviço) estão ocorrendo ao mesmo tempo. Após adicionar a nova chegada na fila, geramos o próximo tempo interchegada e anulamos TA. No outro lado do diagrama, os papéis de TS e TA são naturalmente invertidos.
Esta abordagem é denominada técnica do evento crítico. Uma pequena modificação seria simular o tempo da próxima troca no sistema e então fazer o que a troca determina - alterando o tamanho da fila. Outra abordagem para gerenciar o tempo em simulações de computador é chamado método da fatia de tempo. Ela envolve a escolha de incrementos fundamentais pequenos de tempo, que continuamente atualizam o relógio, e para cada atualização percorrem o programa computando o seu novo estado, baseado sempre no estado atual.
O coração do método de Monte Carlo é a geração de novos eventos através da técnica da função inversa. Virtualmente qualquer distribuição, seja teórica na forma de uma função computável ou empírica na forma de um histograma cumulativo, pode ser usada. Com uma estrutura um pouco mais complicada do que a anteriormente vista, qualquer número de caixas pode ser simulado. De fato podemos simular uma multiplicidade de filas, ou uma grande fila única alimentando uma multiplicidade de caixas. Os mais modernos bancos têm adotado esta técnica que sempre gera tempos de atendimento menores. Este sistema também pode ser simulado como uma extensão das técnicas vistas acima.
Existe uma linguagem de propósito especial, denominada GPSS, que é feita para simular sistemas com múltiplas filas, e vários outros tipos de estruturas. É freqüentemente muito mais fácil escrever programas de simulação nestas linguagens, ainda que o tempo de execução costume ser maior do que quando se usam programas especialmente escritos em FORTRAN ou PASCAL.